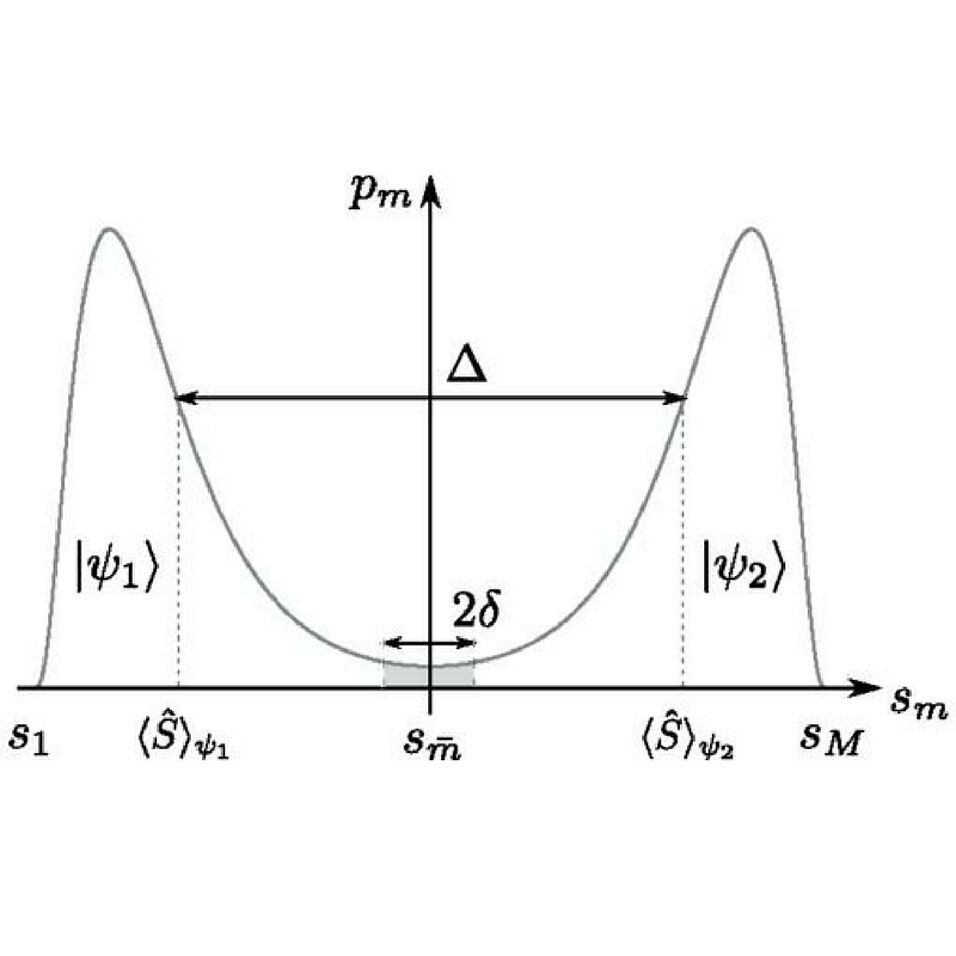
We study the question of what kind of a macroscopic superposition can(not) naturally exist as a ground state of some gapped local many-body Hamiltonian. We derive an upper bound on the energy gap of an arbitrary physical Hamiltonian provided that its ground state is a superposition of two well-distinguishable macroscopic “semiclassical” states. For a large class of macroscopic superposition states we show that the gap vanishes in the macroscopic limit. This in turn shows that preparation of such states by simple cooling to the ground state is not experimentally feasible and requires a different strategy. Our approach is very general and can be used to rule out a variety of quantum states, some of which do not even exhibit macroscopic quantum properties. Moreover, our methods and results can be used for addressing quantum marginal related problems.

view full text here

Borivoje Dakić and Milan Radonjić

Phys. Rev. Lett. 119, 090401