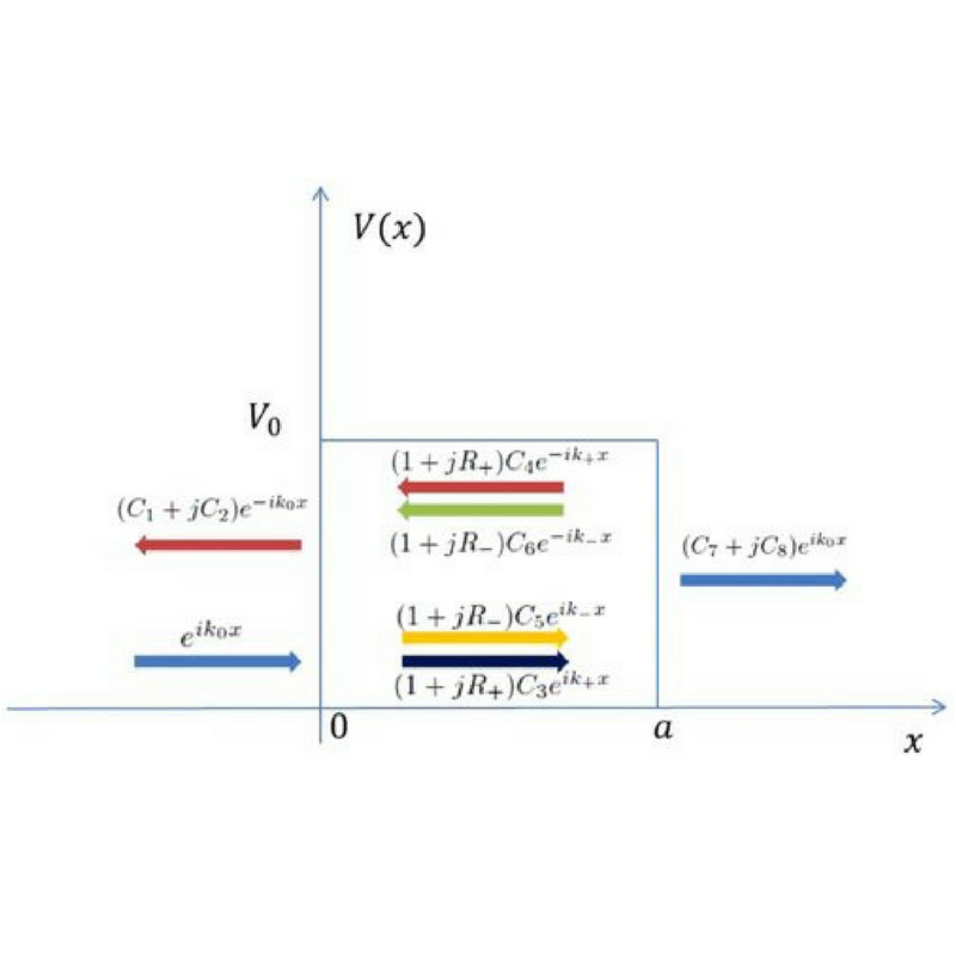
In his recent article [Phys. Rev. A 95, 060101(R) (2017)], Adler questions the usefulness of the bound found in our experimental search for genuine effects of hypercomplex quantum mechanics [Nat. Commun. 8, 15044 (2017)]. Our experiment was performed using a black-box (instrumentalist) approach to generalized probabilistic theories; therefore, it does not assume a priori any particular underlying mechanism. From that point of view our experimental results do indeed place meaningful bounds on the possible effects of “postquantum theories,” including quaternionic quantum mechanics. In his article, Adler compares our experiment to nonrelativistic and Möller formal scattering theories within quaternionic quantum mechanics. With a particular set of assumptions, he finds that quaternionic effects would likely not manifest themselves in general. Although these assumptions are justified in the nonrelativistic case, a proper calculation for relativistic particles is still missing. Here, we provide a concrete relativistic example of Klein-Gordon scattering wherein the quaternionic effects persist. We note that when the Klein-Gordon equation is formulated using a Hamiltonian formalism it displays a so-called “indefinite metric,” a characteristic feature of relativistic quantum wave equations. In Adler's example this is directly forbidden by his assumptions, and therefore our present example is not in contradiction to his work. In complex quantum mechanics this problem of an indefinite metric is solved in a second quantization. Unfortunately, there is no known algorithm for canonical field quantization in quaternionic quantum mechanics.

View full text here.

Lorenzo M. Procopio, Lee A. Rozema, Borivoje Dakić, and Philip Walther
Phys. Rev. A 96, 036101